Homework 4: QuadTree Compression

Due by 11:59PM ET on Monday, October 7, 2024

Required Problems (100 points)

Setup and Logistics

We have put together several stub files –– click here to download them.

2 files to submit: QuadTreeNodeImpl.java and QuadTreeNodeImplTest.java
Please do not submit any additional files.

Be sure to follow these guidelines:

• Ensure source files are not located in any package and that none of the files have a package declaration (e.g. package src;).
• When submitting, submit each file individually at the root level (not contained in a folder or zip files).
• Ensure that your own test files pass and do not run into infinite loops.
• You have unlimited submissions until the deadline on the autograder marked [compilation], and two free submissions on the autograder marked [full].
• For this assignment:
  • Number of Free Submissions: 2
  • Deduction Per Additional Submission: 10 points
  • Max Code Coverage Deduction: up to 10 points
  • Max Style Score Deduction: up to 5 points
  • Manual TA Efficiency/Style Grading: yes
• Do not wait until the last minute to try submitting. You are responsible for ensuring your submission goes through by the deadline.
• Before asking questions on Piazza, be sure to check and keep updated with the pinned clarifications post.
• Gradescope issues? Be sure to check out our Gradescope help page before posting to Piazza.

Motivation - Image Compression

Today’s computers are constantly communicating over the network, transmitting both raw application information and user created data in the form of large files. High-latency networks affect everything from multiplayer video games to standard internet access to life-critical applications.

We cannot always make an Internet link faster (the networked equivalent of throwing more hardware at the problem). Therefore, we must use intelligent algorithms to reduce our load on the network. Some of these are built directly into the internals of our computers, like TCP congestion control. Others are optionally implemented at the application level, such as compression algorithms.

In this assignment, you will implement a relatively simple lossless image compression algorithm based on quadtrees to decompose the image. You will apply similar recursive ideas you learned from HW0 to implement different methods within the QuadTree class. This will be a practical application of your experience working with finding, inserting, and deleting items in binary trees, expanded to four children instead of two.

Learning Objectives

• Understand how to apply recursion effectively to new algorithms
• Expand on your knowledge of data structures in Java
• Gain experience with lossless compression algorithms
• Familiarize yourself with Java syntax and libraries

Quadtree Overview

The simplest way to represent an image is to have a structure that maps every pixel in the image to a color. This is commonly known as a bitmap image. However, for large images this quickly becomes very inefficient. Take the example of a document scanned at a high resolution: Most of the page would be white pixels, and clumps of text would be black and gray pixels. Recording each white pixel of the page separately is very wasteful compared to telling the computer some region of an image should be white.

One solution is to extend this uniform region representation recursively. Instead of defining an image as a collection of arbitrary regions, we define an image as a collection of chunks. Each chunk, in turn, can either be a single color region (blank area) or collection of some other chunks. The end result of this is, of course, a tree like structure, where the entire image is represented by the root chunk and any internal nodes represent chunks that were subdivided. In this model, leaf nodes would represent uniform areas of color.

In general, splitting up chunks is not a very easy task since images come in all sorts of dimensions. We will make the following simplifications and clarifications for this assignment:

• We will only consider square images. Moreover, images will always have row and column sizes that are non-negative powers of 2. That way, they can always be divided into four quadrants of equal size (excluding the case of a $1 \times 1$ region).

• A region will be considered uniform only if every pixel in it has the exact same color. As such, our compression will be lossless, meaning you will be able to exactly decompress the original image.

• Since we are recursively splitting our image into four quadrants of equal size, this kind of tree is called a quadtree. You should use the supplied enum QuadTreeNode.QuadName to refer to each of the four quadrants.

To recap, we have defined a quadtree structure with leaves and non-leaves. Leaves are defined to be nodes with no children and a color. Non-leaves always have four child nodes. Notice that this definition of a quadtree guarantees a full tree; leaves have zero children, and parents have four children.

Now, how do we represent color? The Java BufferedImage class, which we look to for inspiration, stores RGB values as a single combined integer. We use that representation here. You don’t have to worry about how to generate that representation, but just know this is the reason why colors are represented as int s in this assignment. Note that 0 is a valid color in this representation.

Part 0: Read and understand the requirements

Understanding the problem is the first step to solving it. Take time to read through this writeup and the Javadocs for the provided interfaces completely before starting. Refamiliarize yourself with Java syntax and the CIS 121 style guide. Write some test cases to make sure you understand our interface. Make sure you fully read through and understand the assignment before you try to code anything up. Also don’t forget to refer to the JavaDoc in the stub files, as it specifies details to your implementation.

Part 1: Constructing your tree

For this part, you are asked to implement the buildFromIntArray method and the constructor(s) for QuadTreeNodeImpl. The buildFromIntArray method should call your package-private constructor(s) to build a tree that satisfies the quadtree invariants. It is not required, but we encourage you to use package-private helper methods here and for the rest of the assignment. For the rest of the assignment, $n$ represents the number of pixels in the original image.

Your recurrence for building the full quadtree from int image[][] must be $T(n) = 4 T(\frac{n}{4}) + O(1)$. Any algorithms slower than this may time out on our autograder (and/or have additional manual deductions).

Traditionally, computer monitors render the image from top to bottom by filling in each line, so in computer graphics, a flipped coordinate system with the y-axis pointing downwards is used to coordinate points in the image. This means that (0, 0) refers to the top left corner of the image. We will be using a row-major order coordinate addressing scheme, which means that when getting a value, we first index into the correct row, and then index into the column. For example, with the following array

int[][] image = {
        {0, 1, 2, 3},
        {4, 5, 6, 7},
        {8, 9, 0, 1},
        {2, 3, 4, 5}
    };

we can access the value 7 with image[1][3]. In general, the $(x, y)$ coordinate of the image corresponds to image[y][x].

Also note how the QuadName enum works: in this example, the BOTTOM_LEFT of the root quadtree node corresponds to the submatrix

{
  {8, 9}
  {2, 3}
}

We’re leaving this part of the design up to you, so make sure to spend some time planning out how you want to build things. There are many ways to structure your implementations - some will make your life much easier. Note that your constructor can have any signature as our tests will not directly invoke your constructor.

Part 2: Finishing up the tree abstraction

Now that we’ve done the lower-level implementation of the compression tree, we can move onto implementing more interesting methods on the compression tree itself. You will notice that QuadTreeNode.java has a getCompressionRatio() stub. The compression ratio is $\frac{N}{P}$, where $N$ is the total number of nodes in the tree and $P$ is the number of pixels in the image. Your implementation for getCompressionRatio() should run in $O(n)$ time.

For example, given an image with $n$ pixels…

• …that is purely one color: an optimal tree will have one node, with compression ratio $\frac{1}{n}$.

• …that is half black (left), half white (right): an optimal tree would limit itself to five nodes, one for the root and four quadrants as leaves. In this case, the optimal compression ratio is $\frac{5}{n}$. Note what this implies about counting nodes: when there is a non-leaf, it, as well as its children, are included in the count.

You should be able to get the node count from getSize() , and you should be able to easily calculate the number of pixels in the image from getDimension() (both are methods of the QuadTreeNode interface). Your implementation for getSize() should run in $O(n)$ time and getDimension() should run in $O(1)$ time.

The compression ratio is a good way for programs to determine when to use compression and when not to. For images without any uniform colored regions, quadtrees not only cannot effectively compress them, a quadtree will incur extra overhead which can bring the number of nodes over the number of pixels. Programs in real life scenarios would look at this value and decide whether compressing was worth it.

Part 3: Decompression

Because this compression algorithm is lossless, it is possible to recover the original array of RGB combined values from the compressed quadtree with no loss of information. The decompress() method in the QuadTreeNode interface provides this functionality. Implement this method stub and check that your algorithm is lossless, that is, ensure that the compressed -> decompressed output is identical to the original input. Your implementation should run in $O(n)$ time.

Tip: feel free to use assertArrayEquals(expected, actual) from JUnit in your test suite.

Part 4: Retrieving pixel color and editing the image

Implement the method getColor() in the in your QuadTreeNode implementation. The method returns the color of the pixel at coordinate (x, y) of the image represented by the QuadTreeNode . Please implement this method in-place. In other words, do not convert the quadtree into an array and then index into the array. Traverse the quadtree instead; it’s asymptotically faster and more space-efficient. Your implementation should run in $O(\lg n)$ time.

Next, write the method setColor() in the QuadTreeNodeImpl. This method is trickier than the previous one in that it performs an in-place modification of the quadtree. You should always keep the quadtree optimal (i.e., no node should have four children of the same color), which may require compressing nodes or expanding them. You should not have to decompress the whole quadtree in the process of editing the image. Your implementation should run in $O(\lg n)$ time.

To get you started on how to this about adding in this functionality, we’ve provided a few examples. In the following, the color 2 corresponds to light blue, the color 1 corresponds to gray, the color 0 corresponds to white. Consider three cases of what can happen during a call to setColor() :

Case 1: The tree structure does not change

Consider the image below – a call to setColor(7, 0, 2) would simply change the color stored inside the node at image[0][7] representing the top right. Because this color was already different from the color of the coordinates surrounding it, the tree structure will remain unchanged.

Calling setColor(7, 0, 2) will now result in:

Case 2: One or more nodes are broken down into ones representing smaller regions

Consider the image below, with its associated tree structure. A call to setColor(7, 0, 1) would necessitate breaking down the upper right node at image[0][7] into nodes representing smaller regions, in order to store this new color which is different from the rest of the colors in the upper right quadrant. Note that in the resulting tree structure, two levels of children are created for the root’s upper right quadrant, in order to create a leaf that represents a region of dimension 1.

Calling setColor(7, 0, 1) will now result in:

Case 3: Nodes are combined into ones representing larger regions

Consider the image below. In order to ensure that the QuadTree compression is optimal, a call to setColor(7, 0, 1) would result in the combination of the four leaves representing the four coordinates in the upper right corner of the image. This is because there is no longer a need to store them as four separate nodes; they now all have the same color, so they can be stored as one leaf representing a region of dimension 2. This case can be very tricky to implement; as a hint, you may find some overlap with the logic of building the tree from an array source. These similarities may be great candidates to abstract out as helpers. Remember that you’re in charge of designing your implementation.

Calling setColor(7, 0, 1) will now result in:

After implementing this method, you can arbitrarily edit the image without needing to decompress it! That’s pretty cool.

Style & Tests

The above parts together are worth a total of 100 points. Style and code coverage are graded on a subtractive basis with deductions as specified in the Setup and Logistics section of the writeup, and you will be graded according to the CIS 121 style guide. Gradescope will give you your grade on this section immediately upon submission to either autograder.

You will need to write comprehensive unit test cases for each of the classes and methods you implement (including helper methods!) in order to ensure correctness. Make sure you consider edge cases and exceptional cases in addition to typical use cases. Use multiple methods instead of cramming a bunch of asserts into a single test method. Your test cases will be auto-graded for code coverage. Be sure to read the testing guide for some pointers on what level of testing we expect from you. Due to the Code Coverage tools we use, please be sure to use JUnit 4 as it is the only version supported.

Note: You will not be able to write JUnit test cases for any private methods. Instead, make them package-private by leaving off any privacy modifier (i.e., do not write public or private ).

Simple paint!

You will notice that we have included a SimplePaint class. This is a self-contained simple paint application that uses a QuadTreeNode to store an image and allow you to make edits to it by drawing with your mouse. The paint program is built on top of the interfaces provided by quadtrees.

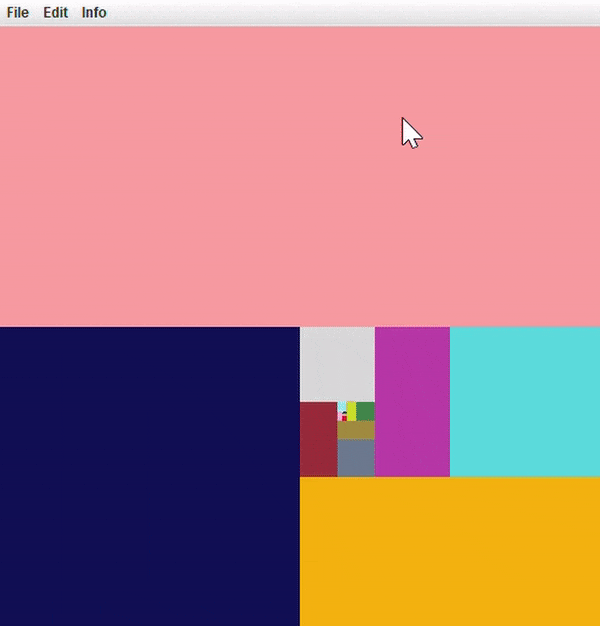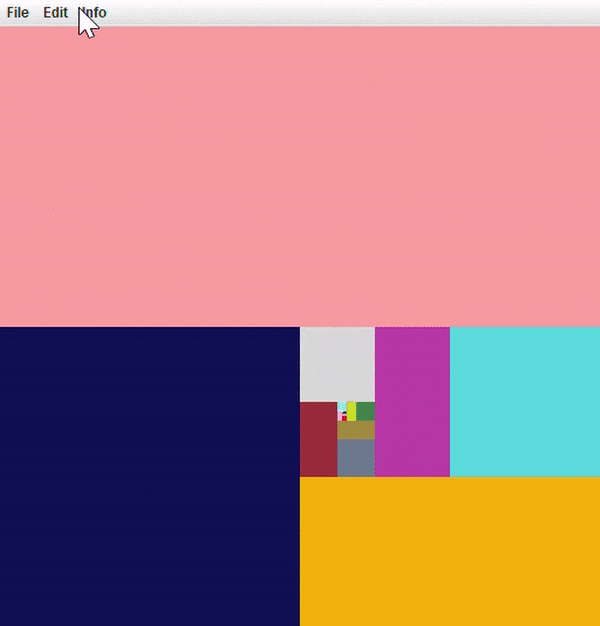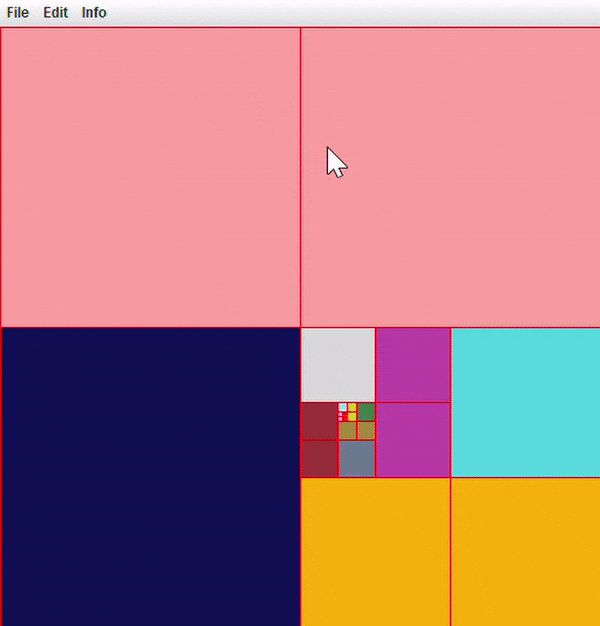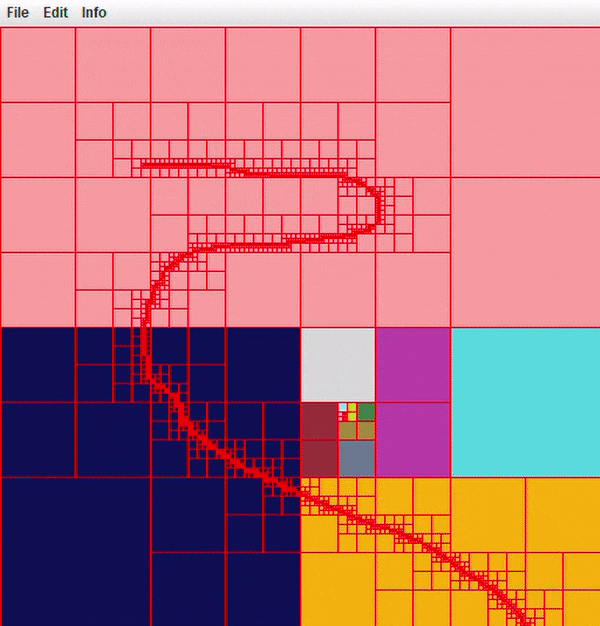
At this point, you should be able to run the program flawlessly. Play around with opening some test images or images of your own. You can also turn on node borders to look at your quadtree structure through this application.

This part is simply meant to be for fun, and there’s no need to include this in unit tests (nor is there an obvious way to do so).

Here’s what SimplePaint should look like if your solution is implemented correctly:

Here is an example after loading a picture into SimplePaint via file/open. Click here to download the sample image.