0. Getting Started

A. Goals

The purpose of the Travelling Salesperson¹ Problem (TSP) assignment is to practice implementing interfaces, manipulating nodes and references, and testing with JUnit. The specific goals are to:

• Implement and use a linked sequence of nodes, a type of recursive data structure.
• Test your implementation with JUnit
• Learn about the Travelling Salesperson Problem, an important theoretical problem in computer science.

B. Background

A travelling salesperson needs to visit each of n cities exactly once, and arrive back home, keeping the total distance travelled as short as possible. In this assignment, you will write a program to find a path connecting n points that passes through each point exactly once.

The travelling salesperson problem is a notoriously difficult combinatorial optimization problem. There does not exist an efficient algorithm to find the optimal tour, the tour of smallest distance. The only way to find the optimal tour is to use brute force: to compute the distance of all possible tours. The problem with this is that there are n! (n factorial) possible tours; enumerating them all and computing their distance would be very slow.

However, there are efficient ways to find a tour that is near-optimal; these methods are called heuristics. You will implement two heuristics to find good (but not optimal) solutions to the traveling salesperson problem. You will also implement a simpler method which creates a tour by traveling to points in order.

1,000 points	Optimal tour through the same 1,000 points

The travelling salesperson problem has a wealth of applications such as vehicle routing, circuit board drilling, circuit board design, robot control, X-ray crystallography, machine scheduling, and computational biology.

C. Your program

In this assignment, you will write a Tour class that models a tour using a ordered sequence of Point objects. You will also write a TourTest class that will contain JUnit tests for Tour.

You will implement the following methods to insert points into a tour.

• In-order heuristic Insert each point at the end of the current tour. This is the easiest to implement.
• Nearest-neighbor heuristic Insert each point into the tour after the point already in the tour which is closest to the point to be inserted.
• Smallest-increase heuristic Insert each point into the tour between the two points which would cause the smallest increase in the total tour distance.

D. Designing the Requirement and Interface

Open the homework on Codio and look at the files provided, or you can download them here. The provided files contain files you can use for testing as well as some helper classes and interfaces you will need:

• TourInterface.java outlines the set of methods that your Tour class will have to implement.
• Point.java is the class for point objects. Each node in the Tour will hold a point object. Point objects are further explained in the next section.
• Node.java represents nodes in your Tour and is also described in the next section.
• VisualizeTour.java is a program that helps you graphically test your Tour class as you write it. It takes a single command-line argument—the name of the data file to use; directions for using it are displayed in the window which will appear when you run it.
• TourTest.java contains JUnit tests for Tour.

To review, look at class and recitation material on nodes, references, linked lists and JUnit.

1. TourTest Class

A. Test Driven Development

In this section we will practice test driven development. In test driven development, we will write test cases in TourTest despite knowing that our tests cases will fail since we haven’t finished Tour yet. Thinking about tests cases in TourTest before implementing Tour will force you to think what exactly the Tour class does, which will help you write better code! In addition, having a test suite ready to go will help you start debugging quickly if some of your tests cases fail.

B. Practicing Test Driven Development

Before writing any code in Tour, read section 2 - Tour Class and section 3 - Insertion Heuristics to get a better sense of what Tour will do and its utility methods. Then you should take a look at TourTest and understand what the given tests cases attempt to test. Some have been filled in for you as well. Your overall process for completing this assignment will be the following:

1. Read the rest of this section, section 2 - Tour Class, and section 3 - Insertion Heuristics to get a good understanding of the Point, Node, and Tour classes and the different insertion heuristics you’re going to implement.
2. Create the file Tour.java and add in method stubs for all of the methods you’ll be implementing from TourInterface.
3. Fill in the test cases in TourTest using your understanding of the methods in Tour and remember to add a class header to TourTest as well. We encourage you to add any of your own tests cases.
4. Implement and complete Tour, running your test cases as you go.

Note: Doing the above is a recommendation, not a requirement. If you decide not to follow the above procedure, that’s okay, but you should instead complete the homework following the order of the writeup. However, we really suggest that you to practice test driven development by following the process above.

C. Test, Test, and Test Again

Don’t be afraid to include more of your own tests. Run your tests often; running them after completing your implementation of a function or making a change is a good idea. Ideally, you should complete all the tests in TourTest, then run them whenever you finish a function in Tour.

2. Tour Class

In this section, you will write Tour, implementing TourInterface. The Tour is represented by a linked sequence of nodes. Each node contains a point which is essentially just a coordinate. Make sure you understand the distinction between the Tour, nodes, and points after reading section 1.

A. The Point Class

The Point class file that represents a point, contained by a node, in a tour. Open it in Codio and study it carefully. The API is as follows:

public class Point
----------------------------------------------------------------------------------------
Point(double x, double y)       // create the Point (x, y)
String toString()               // return String representation
void draw()                     // draw Point using PennDraw
void drawTo(Point that)         // draw line segment between this Point and that
double distanceTo(Point that)   // return Euclidean distance between this Point and that 

B. The Tour Class

Create a skeleton for your Tour class, which must implement TourInterface:

public interface TourInterface
----------------------------------------------------------------------------------------
String toString()               // create a String representation of the Tour
void draw(Point p)          // draw the Tour using PennDraw
                            // any edge starting or ending at p 
                            // should be in a distinct color
int size()                      // number of Points in this Tour
double distance()               // return the total distance of the Tour
void insertInOrder(Point p)     // insert p at the end of the Tour
void insertNearest(Point p)     // insert p using the nearest neighbor heuristic	
void insertSmallest(Point p)    // insert p using the smallest-increase heuristic

Write method stubs for each method declaration in the TourInterface interface. The stubs for methods with non-void return types must each return a dummy value so that Tour.java compiles.

Add appropriate header comments and method comments.

C. The Node Class

The Node class we have provided will form the basis of your Tour class’s node sequence structure. Each Node stores a single Point in your Tour’s path and a reference to the next Node in the path. Its API is as follows:

public class Node
--------------------------------------------------------------------------------------
Node(Point p)                // create a Node containing Point p
Node(Node n, Point p)        // create a Node containing Point p and   
                             // with n as its next Node in the list

Declare (do not initialize yet) the following private fields in your Tour class:

• A Node named head. This will represent the first Node in your Tour.
• A Node named lastNode. This will represent the last Node in your Tour. Whenever you append (add) a Node to the end of your Tour, it will be placed just before this Node. Essentially the lastNode never changes once it is initialized, but the node in the penultimate position of the tour can change.

When your Tour class’s sequence of nodes is not empty, both head and lastNode must be different instances of the Node class (two different objects) yet each Node must store the same Point object. That is, there will be two different Nodes in memory each of which contains a reference to one common Point in memory. Note that this is different from having each Node refer to distinct Point objects with equivalent values. The purpose of this is to represent the cyclical nature of the salesperson’s route: it begins and ends at the salesperson’s home. This is a required implementation detail.

You may not use Java’s built-in LinkedList class to implement Tour. You should also not write your own class called LinkedList since your Tour class will handle all functionality related to managing nodes. Tour is not a linked list because it does not implement the List ADT.

D. Constructor and toString()

Implement a single constructor for your Tour class that takes no arguments and creates an empty Tour. This means that both head and lastNode will be null.

toString() returns a String representation of the Tour (the first Point should show up at the end as well, just like it does in your sequence of nodes). Call toString() on each Point to get a String representation of the Point. Your output must match this description exactly in order to pass the autograder tests.

If the Tour is empty (has no Nodes), toString() should return the empty String.

Helpful: If you need to iterate over your sequence of nodes without specifically doing anything to it, you can do the following:

Node curr = head;
while (curr != null) {
    curr = curr.next;
}

Required Testing: If you haven’t already filled in the test case, complete and run testToStringEmpty(). Running the JUnit should show that this test passes if you’ve implemented the test case and toString() properly.

E. insertInOrder()

To facilitate testing, you will need to implement insertInOrder() so you can add Nodes to your tour.

insertInOrder(Point p) adds a node storing Point p as the “last” node of the Tour.

Remember that your Tour class should always maintain lastNode at the end of the node sequence referring to the same Point p as the first node in the tour.

If the Tour is initially empty, make sure that after this method finishes, your Tour contains two Node objects, both referring to the same Point.

You might find the iteration method in section 2D to be helpful again. You may need to modify it — if, for example, you want to end earlier in the Tour, you can modify the while loop condition. You might also find it helpful to write a helper function that inserts a new Node containing a given point after a given Node.

Required Testing: Write a main method in Tour, create a tour, add the 4 points below using insertInOrder(). You’ll be using this tour to test draw() later which doesn’t have any JUnit tests as it’s difficult to check for correct drawings with JUnit.

• a = (0, 0)
• b = (1, 0)
• c = (1, 1)
• d = (0, 1)

The following image shows the structure of the linked sequence these insertions should create:

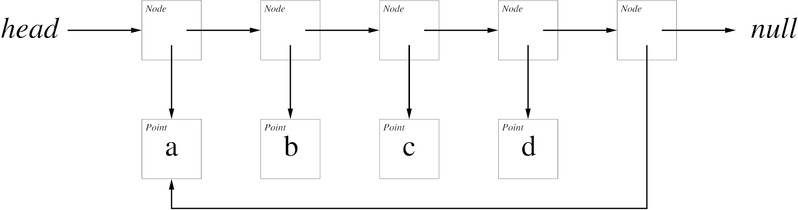
Now call System.out.println on the tour you made, and check that what’s printed matches the following output (including the blank line at the end) by running java Tour in terminal and verify that toString works correctly:

(0.0, 0.0)
(1.0, 0.0)
(1.0, 1.0)
(0.0, 1.0)
(0.0, 0.0)

If you haven’t already done so, complete the remaining toString tests, testToStringOnePoint() and testToStringSquare() in TourTest.

For testToStringOnePoint(), insert a point (0.0 , 0.0) into an empty tour and test what toString() outputs on that tour. The expected correct output should be the string below. Note that \n is a special character that represents a newline and the last newline character is intentional.

String expected = "(0.0, 0.0)\n(0.0, 0.0)\n";

For testToStringSquare() insert the same 4 points as the square tour you created in main of Tour using insertInOrder() and checking that using toString() on the tour gives the correct output. We again have provided the expected correct output:

String expected = "(0.0, 0.0)\n(1.0, 0.0)\n(1.0, 1.0)\n(0.0, 1.0)\n(0.0, 0.0)\n"

If you haven’t done so, run and check that the tests you’ve just completed pass.

F. Utility Methods

Implement the size(), distance(), and draw() methods of Tour. There are many good ways to implement these methods, using for loops, while loops, or recursion. The choice is up to you.

size() returns the number of Points in the Tour, (counting the point in head and lastNode only once). This is distinct from distance()!

distance() returns the total length of the Tour from Point to Point. Use the distanceTo(Point p) method of a Point to find its distance to p. An empty Tour has a distance of 0.0. This is not the same as the number of points in the Tour.

draw(Point p) draws the entire Tour from Point to Point using functions that call PennDraw code. Both edges adjacent to the input Point p should be drawn in a different color (if p is null, none of the edges should be in a different color). Use the drawTo(Point q) method of a Point to draw a line from it to q. As we have provided VisualizeTour to handle setting up PennDraw’s canvas for drawing your Tour, all this function needs to do is call the drawTo method to draw every line segment between adjacent Points. If an empty Tour calls the draw method, the method should simply return without drawing anything.

The image below shows what our reference draws when we call tour.draw(a) (refer to section E for the value of a). tour is the four-point Tour we created for testing. Notice that the lines for a are colored red.

Required Testing: Complete and run all tests for size(), distance(), and insertInOrder() in TourTest that aren’t filled in. Important: Note that the first line of each .txt file are sizing numbers PennDraw uses, not a point, so make sure to account for that in your tests. There are no tests for draw() as it’s difficult to test that items are drawn correctly on the canvas with PennDraw. However, you should verify that your implmentation of draw() works on the four-point Tour that you created in main in part E by using View Running Program, etc. and checking it matches the image above.

As you debug your code, you may find this Java execution visualizer helpful.

3. Insertion Heuristics

A. Testing with VisualizeTour

The VisualizeTour program included provides a user interface for you to visually test the methods you have written in Tour. Run it with a filename argument (one of the files we provide) in the terminal to animate the construction of your Tour. In the table at the bottom of this page, we have listed the values of size() and distance() that your methods should obtain for each insert method, as well as the PennDraw output that draw() should produce.

Required Testing: Check that your in-order insertion method works for at least the input files tsp0.txt, tsp1.txt, tsp2.txt, tsp3.txt, tsp4.txt, tsp5.txt, tsp8.txt, tsp10.txt, and tsp100.txt. Both the drawing itself, and the size and distance, need to match the reference outputs at the bottom of the page. Since you should have passing test cases for functions that you’ve completed so far, you shouldn’t have too many cases that don’t match the given drawings, sizes, and distances. Do not continue until insertInOrder works for all these cases!

B. insertNearest()

insertNearest(Point p) adds a Node storing the Point p to the Tour after the closest Point (Node) already in the Tour.

If there are multiple closest Points with equal distances to p, insert p after the first such Point in the sequence.

Your method must handle empty tours in the same way that insertInOrder() does when there are no nodes in the sequence.

Required Testing: If you haven’t done so, complete and run the insertNearest() test cases in Tour making sure the cases pass. Important: Again, you should note that the first line of each .txt file are sizing numbers PennDraw uses, not a point, so make sure to account for that in your tests. You should also make sure your VisualizeTour results match the figures below for the Nearest-Neighbor Heuristic for all test cases through tsp100.txt like you did for insertInOrder(). Both the drawing itself, and the size and distance, need to match.

C. insertSmallest()

insertSmallest(Point p) adds a Node storing Point p to the Tour in the position where it would cause the smallest increase in the Tour’s distance.

Do not compute the entire Tour distance for each position of p. Instead, compute the incremental distance: the change in distance from adding p between Points s and t is the sum of the distances from s to p and from p to t, minus the original distance from s to t.

Essentially, for each point p that we add, we want to check what the change in distance would be between points s and t in the tour if we were to add p between them, find where in the tour that change in distance is minimized, and put p at that place.

If there are multiple positions for p that cause the same minimal increase in distance, insert p in the first such position.

Your method must handle empty tours in the same way that insertInOrder() does when there are no nodes in the sequence.

If you wrote a helper function when writing insertInOrder() that inserts a given Point after a given Node, you may find it useful again here.

Comment out all print statements in Tour before running VisualizeTour on a file of more than 100 Points. Otherwise, you will be waiting for a long time for VisualizeTour to finish.

Required Testing: If you haven’t done so, complete and run the incomplete insertSmallest() test cases in Tour making sure the cases pass. Important: Reminder that you should note that the first line of each .txt file are sizing numbers PennDraw uses, not a point, so make sure to account for that in your tests. You should also make sure your VisualizeTour results match the figures below for all test cases through tsp100.txt like you did for the other two insertion functions. Both the drawing itself, and the size and distance, need to match.

D. Reference Output

Test your nearest-neighbor heuristic and smallest-increase heuristic methods using VisualizeTour. The following are the values and PennDraw output that your Tour methods should give for each of the provided input files. Note that for the files containing large quantities of points, such as mona-50k.txt, your program may take a long time to build the tour. You may have to wait for several moments, staring at a blank white PennDraw canvas, before your tour is visualized.

File	In-Order Insertion('o')	Nearest-Neighbor Heuristic('n')	Smallest-Increase Heuristic('s')
tsp0.txt	Size: 0 Distance: 0.0000	Size: 0 Distance: 0.0000	Size: 0 Distance: 0.0000
tsp1.txt	Size: 1 Distance: 0.0000	Size: 1 Distance: 0.0000	Size: 1 Distance: 0.0000
tsp2.txt	Size: 2 Distance: 632.46	Size: 2 Distance: 632.46	Size: 2 Distance: 632.46
tsp3.txt	Size: 3 Distance: 832.46	Size: 3 Distance: 832.46	Size: 3 Distance: 832.46
tsp4.txt	Size: 4 Distance: 963.44	Size: 4 Distance: 956.06	Size: 4 Distance: 839.83
tsp5.txt	Size: 5 Distance: 2595.1	Size: 5 Distance: 2595.1	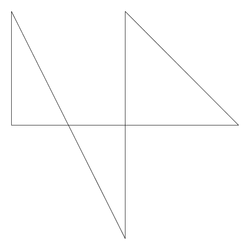Size: 5 Distance: 1872.8
tsp8.txt	Size: 8 Distance: 3898.9	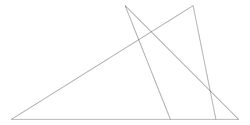Size: 8 Distance: 3378.8	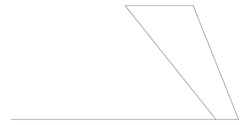Size: 8 Distance: 2545.6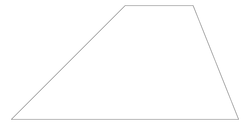
tsp10.txt	Size: 10 Distance: 2586.7	Size: 10 Distance: 1566.1	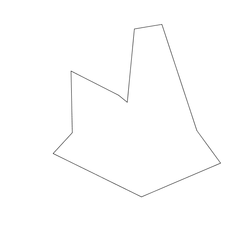Size: 10 Distance: 1655.7
tsp100.txt	Size: 100 Distance: 25547	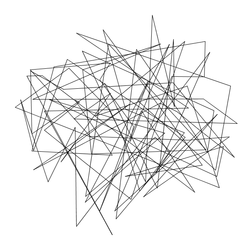Size: 100 Distance: 7389.9	Size: 100 Distance: 4887.2
tsp1000.txt	Size: 1000 Distance: 3.2769e+05	Size: 1000 Distance: 27869	Size: 1000 Distance: 17266
bier127.txt	Size: 127 Distance: 21743	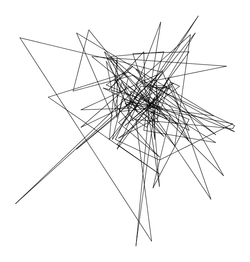Size: 127 Distance: 6494.0	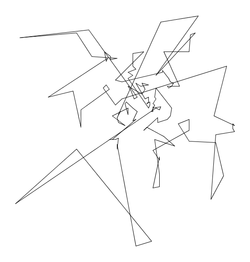Size: 127 Distance: 4536.8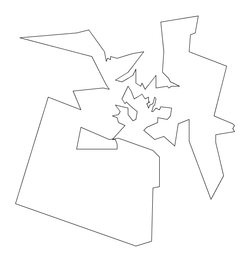
circuit1290.txt	Size: 1290 Distance: 4.303e+05	Size: 1290 Distance: 25030	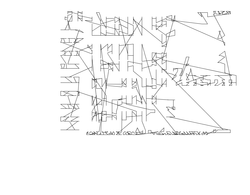Size: 1290 Distance: 14596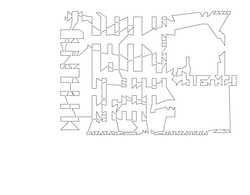
germany15112.txt	Size: 15112 Distance: 4.2116e+06	Size: 15112 Distance: 93119	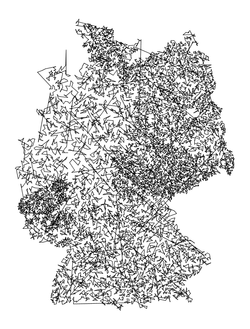Size: 15112 Distance: 55754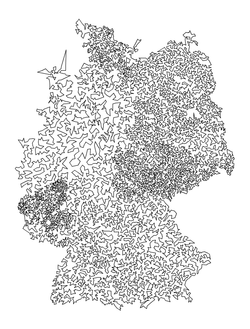
mona-20k.txt	Size: 20000 Distance: 4.9650e+06	Size: 20000 Distance: 94894	Size: 20000 Distance: 56334
mona-50k.txt	Size: 50000 Distance: 1.2366e+07	Size: 50000 Distance: 1.6168e+05	Size: 50000 Distance: 95598
mona-100k.txt	Size: 100001 Distance: 2.4795e+07	Size: 100001 Distance. 2.6272e+05	Size: 100001 Distance: 1.5472e+05
usa13509.txt	Size: 13509 Distance: 3.9108e+06	Size: 13509 Distance: 77450	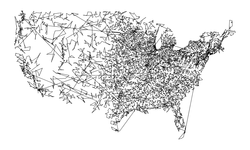Size: 13509 Distance: 45075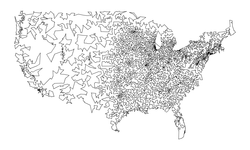

4. Extra Credit

A. Extra Credit

For extra credit, implement a better heuristic in a class TourEC that implements the TourECInterface interface. You are not required to use the Tour or Point classes for your extra credit solution. If you use a modified version of these classes to implement TourEC, include them in your extra.zip; otherwise, your TA may be unable to compile your code.

Be warned that this is a relatively difficult extra credit, although it gives an opportunity to learn a great deal about an extremely important problem. Try to write a TourEC that implements one of the heuristics below.

Here are some heuristics you may choose to implement.

Farthest insertion The farthest insertion heuristic is just like the smallest increase insertion heuristic described in the assignment, except that the Points need not be inserted in the same order as the input. Start with a Tour consisting of the two Points that are farthest apart. Repeat the following:

• Among all Points not in the Tour, choose the one that is farthest from any Point already in the Tour.
• Insert that Point into the Tour in the position where it causes the smallest increase in the distance.

You will have to store all of the unused Points in an appropriate data structure, until they get inserted into the Tour. If your code takes a long time, your algorithm probably performs approximately n3steps. If you’re careful and clever, this can be improved to n2 steps.

Node interchange local search Run the original greedy heuristic (or any other heuristic). Then, repeat the following:

• Choose a pair of Points.
• Swap the two Points in if this improves the Tour. For example if the original greedy heuristic returns 1-5-6-2-3-4-1, you might consider swapping 5 and 3 if the Tour 1-3-6-2-5-4-1 has a smaller distance.

Writing a function to swap two nodes in a linked sequence of nodes provides great practice. Be careful, it can be a little trickier that you might first expect (e.g., make sure your code handles the case when the two Points occur consecutively in the original Tour).

Edge interchange local search Run the original greedy heuristic (or any other heuristic). Then, repeat the following:

• Choose a pair of edges, say 1-2 and 3-4.
• Replace them with 1-3 and 2-4 if the resulting Tour 1-3-6-2-5-4-1 has a smaller distance.

This requires some care, as you will have to reverse the orientation of the links in the original Tour between Nodes 3 and 2. After performing this heuristic, there will be no crossing edges in the Tour, although it need not be optimal.

B. Enrichment

• The best known tour for tsp1000.txt is a solution of distance 15476.519, which was found using the Concorde TSP solver.
• Georgia Tech’s TSP site contains a wealth of interesting information including many applications of the TSP and two TSP games.
• Here’s a 13,509 city problem that contains each of the 13,509 cities in the continental US with population over 500. The optimal solution was discovered in 1998 by Applegate, Bixby, Chvatal and Cook using theoretical ideas from linear and integer programming. The following 15,112 city problem was solved to optimality in April, 2001, and is the current world record. It took 585,936,700 CPU seconds (along with a ton of cleverness) to find the optimal tour through 15,112 cities in Germany.
• Some folks even use the TSP to create and sell art. Check out Bob Bosch’s page. You can even make your own TSP artwork.
• Here is a New York Times article on finding an optimal traveling politician tour in the state of Iowa.
• Here’s a survey article on heuristics for the TSP.

4. Submission

A. Readme

Complete readme_tsp.txt in the same way that you have done for previous assignments.

B. Testing

Double-check to make sure you’ve completed all tests in TourTest.java. Don’t be afraid to add some of your own test cases as well. You should make sure that your tests pass.

C. Submission

Submit Tour.java, readme_tsp.txt, and TourTest.java on Gradescope.

You may also submit a TourEC.java file for extra credit. If your TourEC.java requires any additional files, including a modified Point.java or Tour.java, make sure to submit those as well.