Recursion

Summary of Deliverables

By the end of HW08, here is everything you will need to submit to gradescope:

finger_exercises.py
test_finger_exercises_student.py
readme_recursive.txt
sierpinski.py

0. Getting started

A. Goals

The goal of this assignment is to familiarize you with recursion and give you more practice writing unit tests. Specifically:

Practice writing recursive code
Practice writing recursive functions that utilize helper functions
Revisit writing unit tests

B. Motivation

Recursion is one of the most powerful tools in computer science. It takes a problem that may be very difficult to solve all at once and lets us solve just one part of it. Then we recursively use that logic on the rest of the problem. In the end, we have solved the greater problem just by doing a little bit of work at each step. Recursion can be used to solve enormous problems with just a few lines of code. In fact, there exist problems that can feasibly only be solved recursively! Recursion plays a major role in not just problem solving, but data structures too, which we will see later in the course. Although it’s conceptually difficult, recursion is an incredibly cool and rewarding thing to learn.

Applications to Other Fields

Recursion doesn’t exist only in computer science. Other fields, like math, linguistics, and logic, all use recursion. In linguistics, for example, we can build sentences out of phrases, and these phrases can contain themselves as subphrases. For example, we can have a phrase of “big friendly giant”, which consists of an adjective, “big”, and a subphrase of “friendly giant”, which consists of an adjective, being “friendly”, and a subphrase, being “giant”. This fact means that we can make sentences that are infinitely long - all we have to do is add another level of recursion to our phrases!

C. Overview and Setup

Solutions using iteration (for/while loops) or comprehensions will be given no credit. Most functions are forbidden calls (other than calling your helper or recursively calling) are banned as well.
The only functions that are allowed outside of your own functions & helpers are:

len()
max()
float()

Slicing strings and lists is also allowed.
If you want to use a helper function, it must have the same name as the original function and just have _helper appended to the end of the name. For example if the cow function needs a helper function, it should be called cow_helper.
This includes sort, sorted, sum and others. The autograder will not be happy with print statements. You can print while you work on the code, but remove them once you submit your code.

Overview

In the Recursion Finger Exercise portion of this assignment, you will create a file full of functions that each perform a different task in a recursive fashion. Solutions using iteration (for/while loops) will be given no credit. You are responsible for writing proper docstrings for all the functions you will write.

You are given some unit tests that you can use to test your finger exercise implementation, but you will also need to write some of your own test cases, as the tests you are given are not comprehensive nor representative of the complete testing suite you will be graded with.

In the Sierpinski part of the assignment, you will also use recursion but this time to create a fractal image. You will do this utilizing penndraw and recursion. Like the finger exercises you will be responsible for writing good comments and docstrings, but you will not have to create any unit tests for this. Instead you should be able to test this by making sure the image looks correct when you run it.

Setup

You should create three (initially empty) python files in Codio - finger_exercises.py, test_finger_exercises_student.py and sierpinski.py. You should also see finger_exercises_tests.py, which contains the tests you have been given. If you need the original files, you can download them here.

1. Finger Exercises

For the exercises below, we have provided the function header and problem description. You may find it necessary to write helper functions for these methods if you think you need more input parameters than the provided functions have.

Important: Note that, although there are 7 problems outlined, you only need to choose 5 of them to implement. If you implement more than 5, we will grade the first 5 functions in finger_exercises.py only. Any additional functions will automatically fail the autograder - if you’d like to see the tests for later functions from the autograder, comment out the first ones you did.

Here’s an example of a problem that doesn’t use a helper method:.

def is_palindrome(word):

    // base case - length is 0 or 1, and therefore is a palindrome.
    if (len(word) <= 1):
        return True

    // check if first and last are the same
    first_char = word[0]
    last_char = word[len(word) - 1]
    first_and_last_match = first_char == last_char

    // if they match, recurse on the string without the first and last letters
    return first_and_last_match && is_palindrome(word[1:len(word)-1])

We of course could have solved this with a helper like this:

def is_palindrome(word):
    // return our recursive helper since we want another parameter
    return is_palindromeHelper(0, word);

def is_palindrome_helper(index, word):

    // base case is we are halfway through the word and it's still a palindrome
    if (index >= len(word) / 2 ):
        return True

    first_char = word[0]
    last_char = word[len(word) - 1]
    first_and_last_match = first_char == last_char

    // recurse on rest if they match - otherwise, we will return false
    return first_and_last_match && is_palindrome(index + 1, word)

Both solutions are equally valid - if you want to solve a problem using a helper method, you will not be penalized for doing so if there exists an implementation without the helper. You should approach these problems in the way that makes the most sense to you.

Tip: Remember to start by thinking about the base case — the smallest, simplest problem possible. From there, work out a way to get from a larger input down to the base case.

Tip: Be aware of the invariants that are given. Invariants are properties that will always hold true for the given problem.

Tip: If you can’t decide whether a helper method will help make the solution easier, think about the arguments you want to pass in during a recursive call. If your arguments for a recursive call differ in number or type vs. the header of the function you want to help, think about how a helper can resolve that conflict for you.

A. Greatest Common Denominator (GCD)

Function Header: def gcd(a, b).

Argument(s) and Return Types: a and b are integers, and an integer is returned.

Problem Description: The Greatest Common Denominator (GCD) of two integers, $a$ and $b$, is the largest number that divides both values. One way to solve this problem is to find the prime factorization of both $a$ and $b$ and return the product of the common factors. That way takes a long time, and we can do it smarter! Euclid came up with an algorithm for this problem long before computer science existed.

If $a < b$, return $GCD(b,a)$
If $a = b$, return $b$
If $b = 0$ return $a$.
Otherwise, return $GCD(b, a \% b)$

Invariants: You may assume that $a$ and $b$ are non-negative integers. 0 is a non-negative integer, but you may also assume that it will never be the case that both $a$ and $b$ are 0. However, it is possible for one of the two inputs to be 0. That is, $GCD(0, 5)$ is valid, as is $GCD(5, 0)$, but $GCD(0, 0)$ is not.

Algorithm Explanation: One way to do GCD would be to start at 1 and keep track of the largest number that divides both values at each level. When we do that, we definitely get the right answer. Another way to think about it is subtracting by the smaller value until the bigger number is less than or equal to the smaller number. For example, say we have 40 and 12. 40 - 12 is 28, 28 - 12 is 16, 16 - 12 is 4, so the answer is 4. This process is very similar to take a modulo, as we essentially are finding the remainder after dividing the value.

This relies on the principle that the GCD of two values will not change if you replace the larger one with the difference of the larger and the smaller one. The intuition behind this is that if my GCD divides x and y, then it must be true that it will divide x−y, because x and y are just integer multiples of the GCD, so x−y is equivalent to some integer multiple of the GCD as well! For example, with 40 and 12, the GCD is 4. Let’s have the GCD be z, let 40=x, and 12=y. We therefore can say x−y=10z−3z=7z, and 7z is of course an integer multiple of the GCD!

If you’re still curious to learn more about Euclid’s algorithm, take a look at its wikipedia page, specifically the “Description” and “Proof of Validity” subsections!

B. Cumulative Sum

B.1

Function Header: def sum_between(a, b)

Argument(s) and Return Types: a and b are integers, and an integer is returned.

Problem Description: The goal is to find the sum of the values from $a$ to $b$. In math, we would write this problem as $\sum_{i=a}^{b} i$. You must also do B.2 if you choose this question.

Invariants: You can assume that $a \leq b$ for all inputs.

B.2

Function Header: def sum_to(x)

Argument(s) and Return Types: x is an integer, and an integer is returned.

Problem Description: Now, write another method to find the sum of values from 1 to $x$, inclusive. Think about how you can take advantage of prior code to solve this problem. Remember, you must also do B.1 if you choose this question.

Invariants: You can assume that $x >= 1$.

C. Find Second Largest

In this problem we are being explicit that you need a helper function. We provide the function the user should call, and how it should call the helper function. Your job is to write this helper function.

Function Header: def find_second_largest_helper(largest, second_largest, index, nums)

Argument(s) and Return Types: largest, second_largest, and index are intgers. nums is a list of integers. The function returns an integer.

Problem Description: Given a list of integers, find the second largest value in the list. We are going to be implementing a helper function for this - you should add this to your program as the “public” function (The one that will be directly called by other users) and then write the helper function with the method header presented above. Note that we use float('-infinity') here to pass in a default starting minimum value that will be updated as we find the second largest value.

def find_second_largest(nums):
    return find_second_largest_helper(float('-infinity'), float('-infinity'), 0, nums)

Invariants: You may assume that the list is not None and has at least 2 different elements.

Important: If the list is something like [2, 2, 1], you should return 2. The reason for this is that if we removed the largest element, the new largest element would still be 2.

D. Zig Zag

Function Header: def zig_zag(string, k)

Argument(s) and Return Types: string is a string, k is an integer, and a string is returned.

Problem Description: Write a recursive function that takes a string and a number, and returns a new string. This new string should contain K copies of the original string appended together, but every other copy is reversed. For Example: zig_zag('abc', 2) should return ‘abccba’ and zig_zag('zig', 3) should return ziggizzig

Invariants: You may assume that $k \geq 0$.

E. Count Ways to Climb Stairs

Method Header: def count_ways_to_climb(stairs):

Argument(s) and Return Types: stairs is an integer, and an integer is returned.

Problem Description: Given an amount of stairs to climb, calculate the number of ways to climb taking either 1 or 2 steps at a time. For example, if there are 4 stairs, we would return 5, as there are the following options:

Hint: Write out by hand the possibilities for small examples. See if you notice a pattern you can take advantage of.

1, 1, 1, 1
1, 1, 2
1, 2, 1
2, 1, 1
2, 2

Invariants: You may assume that the stairs >= 0. If stairs is 0, you should return 1.

F. Largest Selection

Method Header: def largest_selection(numbers, choices)

Argument(s) and Return Types: numbers is a list of numbers, and choices is an integer. The function returns a number

Problem Description: We are given a list of numbers and must find what is the largest sum we can get if we have to choose exactly choices amount of the elements from the list.

Examples: Consider the list [3, 1, 2]. If we call our function with that list and choices equal to two (largest_selection([3, 1, 2], 2)) then we must find the largest sum that can be gotten from selecting exactly two elements from the list. in this example, our function call should return 5 since the largeset sum selecting two elements is 2 + 3.

Note that we MUST select exactly choices elements from our list. Consider the list [-5, -3, 2, 6]. If we call our function with choices equal to 3, then our result would be 5. This is because 6 + 2 + -3 is the largest sum when we select 3 of the elements from the list. Note that even though -3 makes our sum smaller, we still must choose it to get up to 3 elements chosen.

Invariants: You may assume that the list is not None and has at least 1 element

Important: If the list is something like [2, 2, 1] and the choices is 4 (e.g. there are more choices than elements in the list), you must return float('-infinity') to indicate that it is impossible to get a sum with that many choices. You may want to use this logic in your code as a base case.

Hints:

Remember that you can use list slicing and process one element at a time
You do not need to do anything “too clever”. Just remember that each element could either be in the selection or not in the selection.

G. CountSubstrings

Method Header: def count_substrings(sequence, word)

Argument(s) and Return Types: sequence and word are strings, and an integer is returned.

Problem Description: We want to find how many times a sequence appears in a particular word.

For example, in the word “banana”, the sequence “na” appears two times, with “banana” and “banaNA”. So count_substrings("na", "banana") should return 2.

If we were to call it on the string "ana" e.g. count_substrings("ana", "banana") then it should also return 2. This is because “ana” also appear two times, with “banana” and “banana”. Note that this means that we can have overlaps between the starts of our sequences (this actually makes the problem easier!)

Invariants: You may assume that neither sequence nor word are None, and that both have positive lengths (0 is not positive.) You may also assume that the strings are both all lowercase.

Hint: String slices will be helpful here.

# Reminder on how string slices work:
class_name = "cis1100"
department = class_name[:3]
number = class_name[3:]
print(department) # prints "cis"
print(number)     # prints "1100"

H. Extra Credit

How Different?

Method Header: def how_different(one, two)

Argument(s) and Return Types: one and two are strings, and an integer is returned.

Problem Description: This is the most interesting problem of what we’ve seen so far. Given two strings, we want to find out what the least amount of changes we would have to make to one of the strings to get to the other. There are three ways we can change a string. 1, we can replace a letter with another letter. 2, we can delete a letter. 3, we can add a letter. Here are some examples to help make this clear.

Example 1: code, coder. We can add one letter to the first string, being an r, to make the strings match, so this should return 1.

Example 2: mouse, must. We see that both share the same first letter, so we don’t have to make any changes there. Then, we can delete the o in mouse, then, the next letter is s for both strings, and then we can change the e into a t to make both into must. That’s a total of 2 changes. There are other ways we could have transformed the first string into the second, but this is the one with the least changes, and that’s what we’re interested in.

2. Part Two: Finger Exercises Tests

For each of the 5 functions you completed in the previous section, you will write one test case to test your code. These test cases should be written in test_finger_exercises_student.py.

A. Motivation

We’ve done test writing in previous assignments already, but writing unit tests is a core part of software development, no matter what programming language you use. Because of this, we are revisiting unit test writing to give you more practice with it. Remember, the best way to get better at something is practicing it.

B. unittest Reminders

As a review, unittest works by comparing what is actually returned by your functions and object state. Here is an example:

import finger_exercises
# above line imports the code we want to test

class ExampleTest(unittest.TestCase):

    def test_sum_between_example():
        """Tests the sum_between function on a simple input"""
        # declare what we will use as input for the test
        first_test_input = 3
        second_test_input = 5

        # get what the actual output is by calling the code we want to test
        actual = finger_exercises.sum_between(first_test_input, second_test_input)

        # declare the expected output:
        expected = 3 + 4 + 5

        self.assertEqual(actual, expected)

You’ll find the following functions from the unittest library useful:

assertTrue(someConditon)
assertFalse(someCondition)
assertEqual(expectedValue, actualValue)

Note that you can put multiple assert statements in one test. With multiple assert statements in a test, if a single one of them fail, the whole test will fail. However for this homework, the use of multiple assert statements is not expected nor needed. Multiple asserts will be useful in future homeworks.

C. Writing Tests

To start, open test_finger_exercises.py and take a look at the test cases that have already been given to you. The test cases that you write yourself must be different than the given cases - credit will not be given to a repeated case.

Write your test cases in test_finger_exercises.py. You are only required to write one new test per function, but we encourage you to write as many tests as you need to feel confident that your code works. Once you’ve written these, run the tests (directions described below) and make sure they pass. We recommend testing your functions with multiple edge cases and varied input arguments to ensure that your code works for all possible scenarios.

D. Running your Tests

To run your tests, all you need to do is go to the terminal where we would normally run our programs and run the following command:

python3 -m unittest test_finger_exercises_student -v

If you want to run the test functions that we give you, all you need to do is replace one part of the command. Instead of test_food_recommneder_student it would just be test_food_recommender:

python3 -m unittest test_finger_exercises -v

If you want to run only some specific tests you can do that by specified further in the command. For example, if I want to run all tests that are in the TestSumBetween class of test_finger_exercises.py, then I could run:

python3 -m unittest test_finger_exercises.TestSumBetween -v

If I wanted to be more specific and run a specific test function within a certain class, I could do that. Lets say I want to runtest_sum_between_one_five within the TestSumBetween class, I could do:

python3 -m unittest test_food_recommender.TestSumBetween.test_sum_between_one_five -v

3. Sierpinski

In this assignment, you will write a program sierpinski.py that recursively draws a Sierpinski carpet using penndraw. These instructions will walk you through the process step by step. You are not allowed to use penndraw.set_scale(), or any scale changing in this assignment. Doing so will only make the assignment harder.

A. The `main()` function

Write a main() function that calls the penndraw.filled_square() function to draw a square with sides of length 1.0 / 3.0 with the center vertex located at (0.5, 0.5). Later, you will modify main() to draw the full Sierpinski carpet.

When you compile and run your program, you should see a square in the center of your window.

(it should look like the first image in the section “E. Checkpoint” below)

B. Setting up the recursive structure of `sierpinski()`

Write a function sierpinski() that takes two parameters, num_levels and half_side_len. These parameters should be numbers. Your function should print both parameters, before recursively calling itself eight times with the arguments num_levels - 1 and half_side_len / 3. The recursion should stop when num_levels is less than 1 or if half_side_len <= 0.001. Later, you will replace the print statements with a call to penn_draw.filled_square().

You should also modify main() to call sierpinski(num_levels, 1.0 / 6.0), where num_levels is the first command-line argument interpreted as an integer. Don’t forget to import the things needed to access command-line arguments!. You may assume that your program will be run with exactly one command-line argument that is a positive integer.

Hint: Think about how many recursive calls you need to make.

C. Checkpoint

Running your program with the following command-line arguments should produce the following output:

python sierpinski.py 0
(no output)

python sierpinski.py 1
1 0.16666666666666666

python sierpinski.py 2
0.16666666666666666
0.05555555555555555
0.05555555555555555
0.05555555555555555
0.05555555555555555
0.05555555555555555
0.05555555555555555
0.05555555555555555
0.05555555555555555

python sierpinski.py 3
0.16666666666666666
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.05555555555555555
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517
0.018518518518518517

D. Drawing the Sierpinski carpet in `sierpinski()`

Comment out the print statements from sierpinski().

Modify sierpinski() to take two additional arguments, x and y, and draw a Sierpinski carpet of order num_levels of size 2 * half_side_len centered at (x, y). Remember that if you have more than 85 characters on a single line, you need to break the line up. This can be done by putting a linebreak between arguments. Your recursive calls may be in any order you like.

Think recursively. A Sierpinski carpet of order num_levels comprises just a solid square and eight smaller Sierpinski carpets, each one third the size of the original, each of order num_levels - 1, to the four cardinal directions plus the four diagonals relative to the center square. The distance between the center of the original square and the center of the smaller squares should be 2 * half_side_len of the original in both the $x$ and $y$ directions. You have already written the function to draw the square and the recursion code from the previous steps – now, you only need to make the correct function calls.

Warning: Do not call penndraw.set_canvas_size(), or penndraw.save(). These functions will break our test scripts, and you will receive a large point deduction.

E. Checkpoint

Running your program with the command-line arguments below should produce the following output.

Input: python sierpinski.py 1

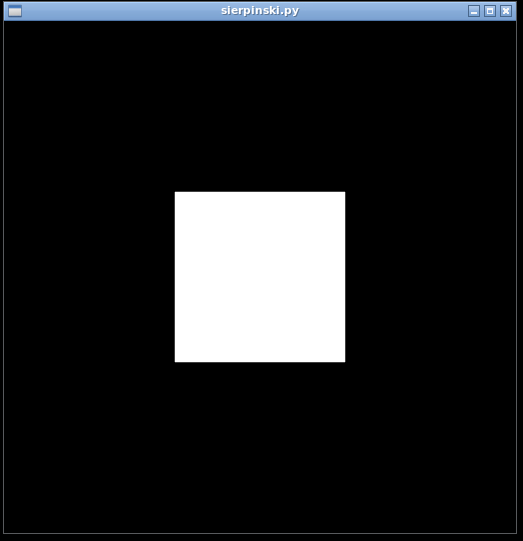
Input: python sierpinski.py 2

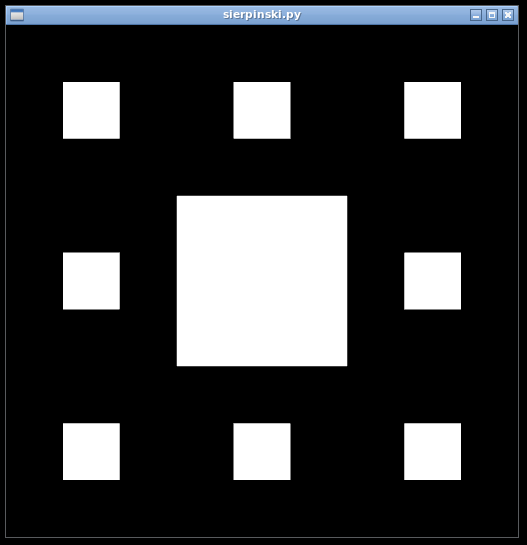
Input: python sierpinski.py 3

Input: python sierpinski.py 4

Input: python sierpinski.py 5

F. Animating [Optional]

Once you have your Sierpinski carpet working, add calls to penndraw.enable_animation() and penndraw.advance() into your sierpinski() function. (You are not required to animate your Sierpinski carpet, and it is not worth any points, but it is fun and will help you visualize the recursion. If you do add animation, leave it in your code: it will not affect our grading scripts.) Experiment with different arrangements of the recursive calls to sierpinski().

4. Readme & Submissions

Please complete the readme and then submit finger_exercises.py, test_finger_exercises_student.py, sierpinski.py, and readme_recursive.txt on Gradescope.

Note that we will only run tests for the first 5 finger exercises you completed - the rest will automatically fail. If your grade is a 20, that means you’ve passed all the tests that you should have. The sierpinski.py file will be graded manually.